Actuarial Simulation - baseVersion
Originating from the DGVFM student/teacher documentation under "werde-aktuar", the free base version 2024 of the Actuarial Simulation app is now available again, significantly expanded, in the APP Store for iOS (iPhone and iPad). While only Poisson and Pareto distributions could be simulated in the 2017 version, significantly more distributions are now available.
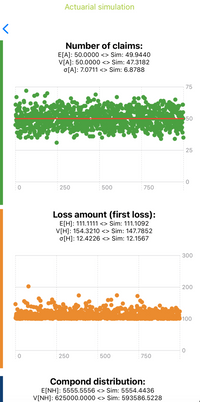
The following distributions are included for the number of claims (frequency):
- Poisson - e.g. λ=50; E[N]=50; σ[N] =50
- Binomial distribution - e.g. n=100; p=0,2; E[N]=20, σ[N] =4
- Negative Binomial distribution - e.g. n=10; p=0,2; E[N]=40; σ[N] =14,1
- Constant values (for teaching and testing purposes)
For the loss amount distributions (severity):
- Pareto - e.g. α=10; t=100; E[H]=111,1; σ[H] =12,4
- Exponential distribution - e.g. λ=0,1; E[H]=10; σ[H] =10
- Normal distribution - e.g. μ=100; σ=20; E[H]=100; σ[H] =20
- LogNormal distribution - e.g. μ=5; σ=0,2; E[H]=151,4; σ[H] =30,6
- Generalized Pareto - e.g. μ=10; σ=1,2; ξ=0,2; E[H]=11,5; σ[H] =1,94
- Gamma distribution - e.g. α=100; λ=2; E[H]=50; σ[H] =5
- Weibull distribution - e.g. β=100; α=2; E[H]=88,6; σ[H] =46,32
- Constant values (for teaching and testing purposes)
With the setting "Constant = 1", e.g. for the frequency distribution, the percentiles of the respective loss amount distribution set can then be analysed. And vice versa.
The threshold value shifts the respective distribution by the entered value.
The number of simulations is currently set to 1000.
After entering the parameters, start the simulation. If the status button is green, the results can be analysed. As long as it is still red, the following pages have not yet been recalculated.
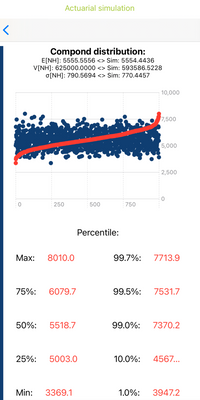
The results are as follows:
The free baseVersion can be found in the APP Store(iOS) under "actuary".